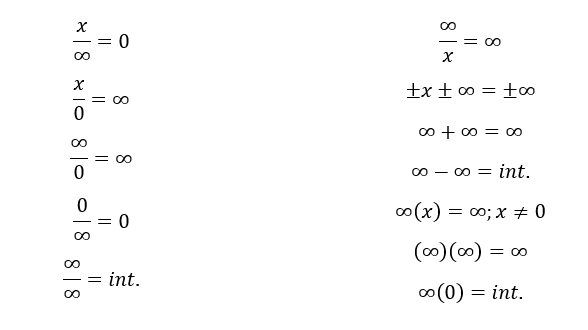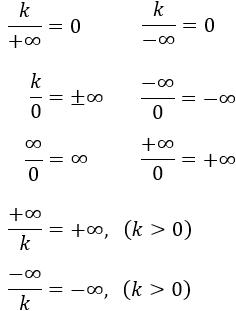Limites E Al Infinito

Porque en teoria e elevado a 1 entre infunito es cero y e elevado a cero es 1 no.

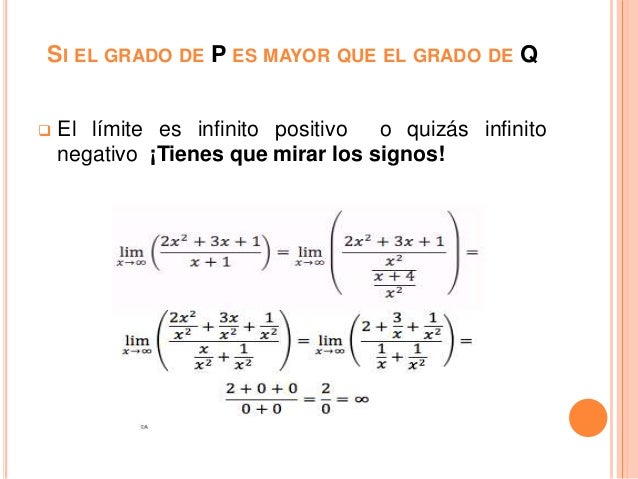
Limites e al infinito. Novamente inicia se com um exercício básico que serve de base para outros exercícios. Para considerar un límite de una función en el infinito tenemos que tener en cuenta una serie de reglas que nos ayudaran a facilitar las operaciones. Ejercicios resueltos de órdenes de infinito. Este tipo de limite nos exige analisar os limites laterais pois no ponto em que devemos calcular o limite a função não está definida.

Observa que la función exponencial crece mas rápido que la potencial y esta que la logarítmica. Así limite e x limite e u limite 1 e u si. E representamos de duas formas. Pero eso es un poco problemático porque si dividimos 1 en infinitas partes y resulta que cada una es 0 qué ha pasado con el 1.

Texto sobre os limites no infinito de uma função matemática como são calculados exemplos gráficos entre outras informações. Si x infinito pongamos u x luego u infinito. Así que 1 es un poco como decir 1 belleza o 1 alto. Limites infinitos e limites no infinito neste post apresenta se a temática dos limites infinitos e limites no infinito que consiste nos casos em que o limite em um determinado ponto resulta em e nos casos em que queremos saber o limite quando.

De hecho 1 es indefinido. No entiendo porque en algunos ejercicios me pone que e elevado a infinito es cero y otro que me da infinito y con e elevado a menos infinito cuanto es. Muchas veces queremos conocer cómo se comporta una función en el infinito en algunas ocasiones es algo complejo hasta abstracto. Exercícios resolvidos de limites que tendem ao infinito.

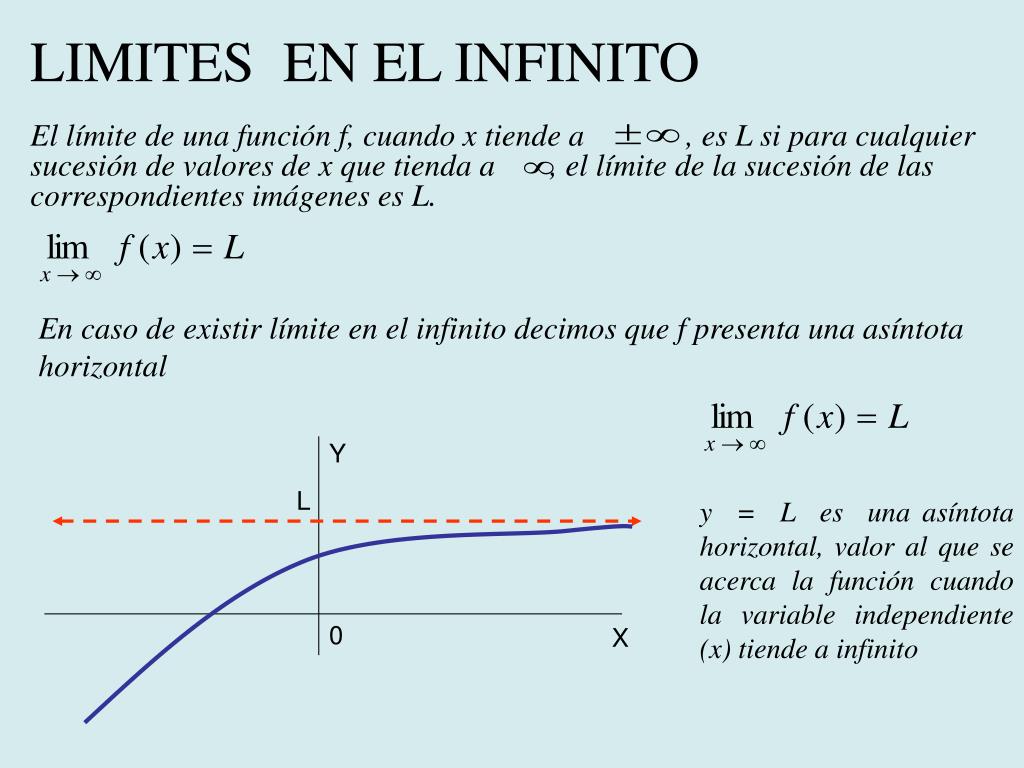
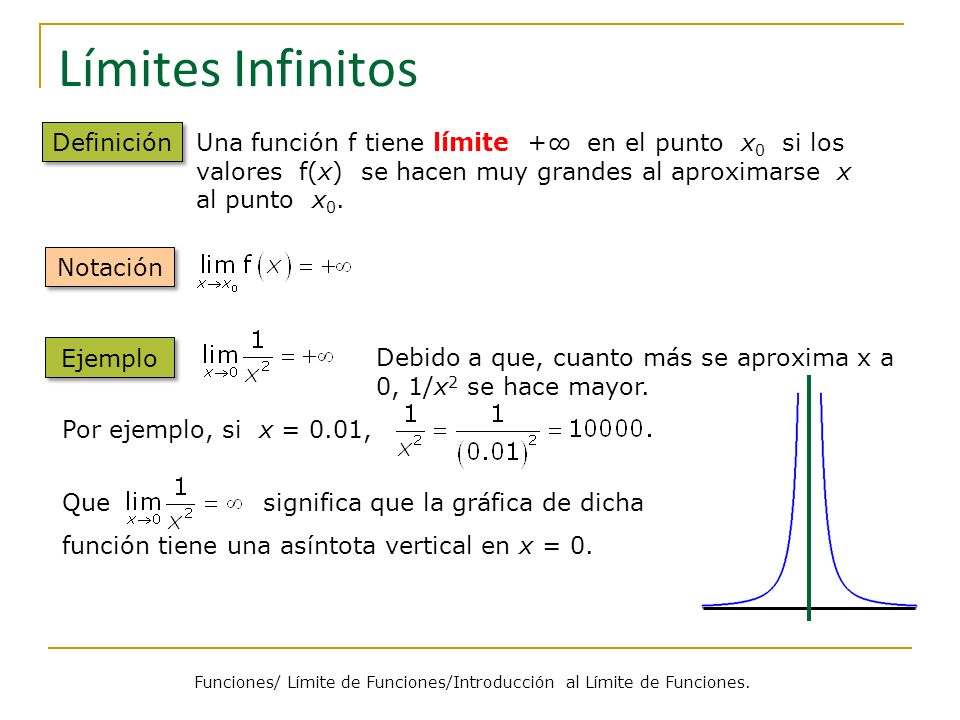
Quieres calcular limite e x cuando x infinito. Todas las funciones tienden al infinito. En la siguiente imagen queda recogido el concepto y la notación que se suele utilizar. Limites no infinito ou tendendo ao infinito são aqueles em que a variável da função tende ao infinito.

Hoy te traemos una investigación con algunos ejemplos del tema límites infinitos y límites al infinito de la materia de calculo diferencial. A lo mejor podríamos decir que 1 0. Por qué no lo sabemos.