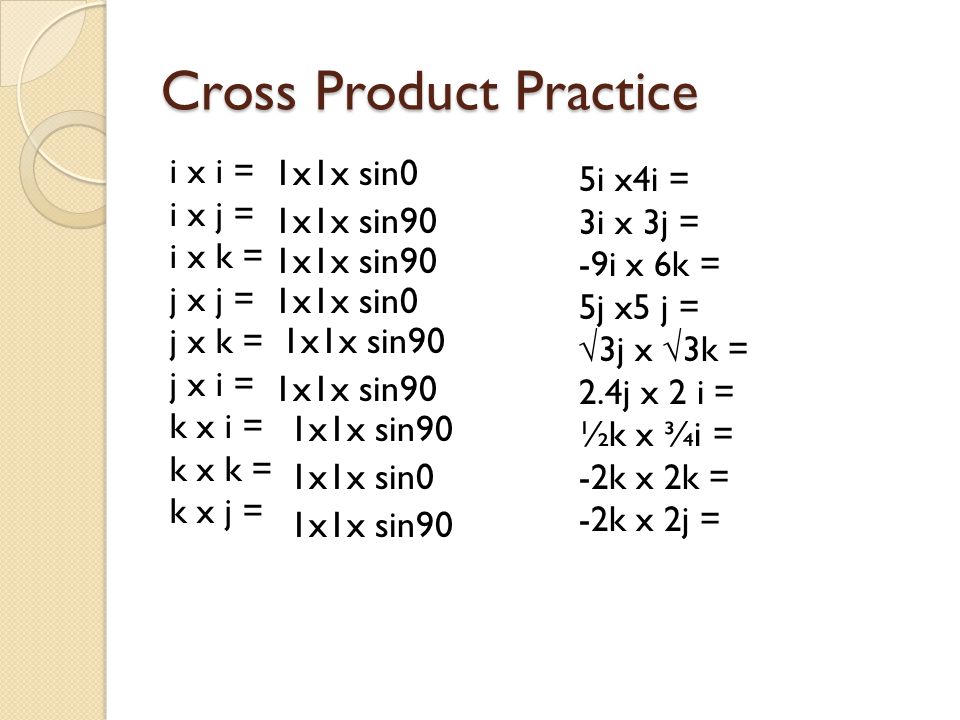K X K Vector

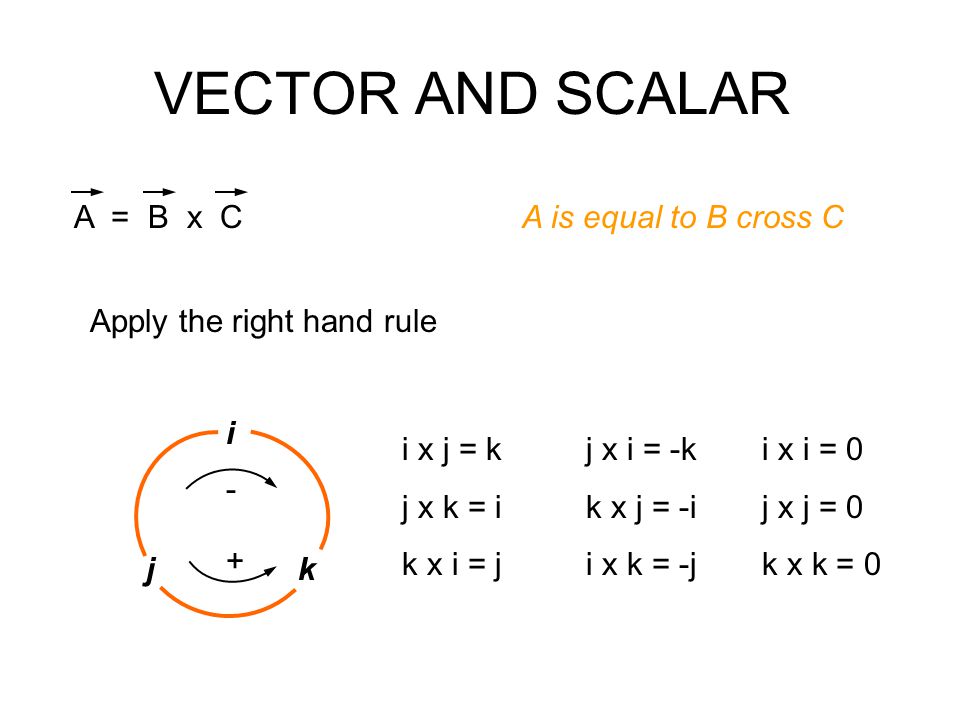
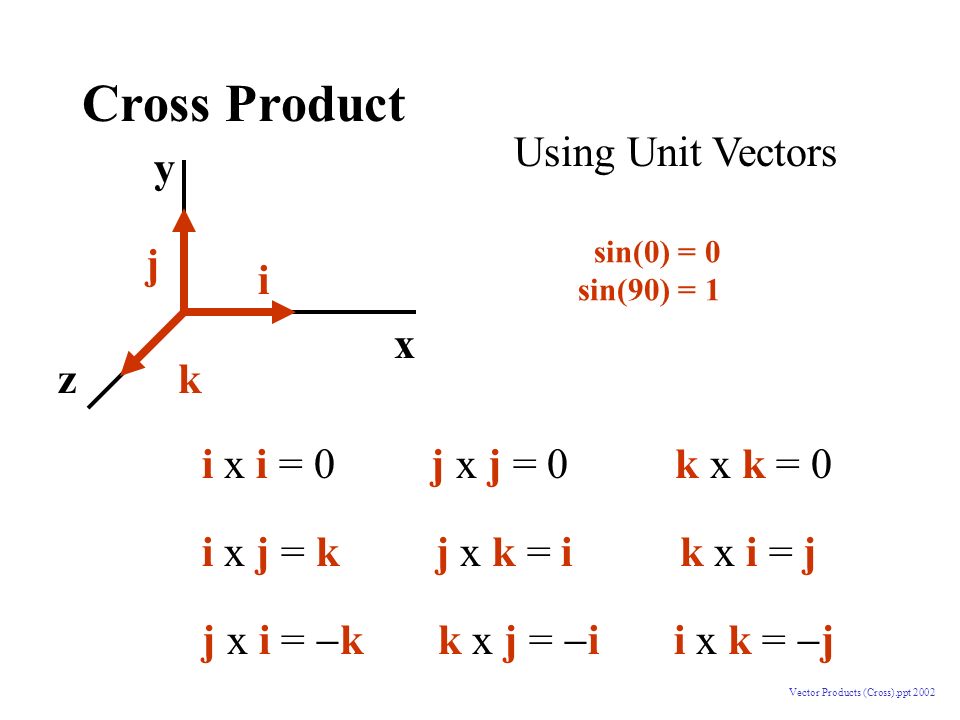
We must also establish the following identities for unit vectors.

K x k vector. Answer to theorem let x be a vector space over k and x 12 x 2 are equivalent norms on it. In a multidimensional system the scalar k x displaystyle kx would be replaced by the vector dot product k r displaystyle mathbf k cdot mathbf r representing the wave vector and the position vector. Use distributive cross multiplication to calculate the cross product. The first row contains i j k.

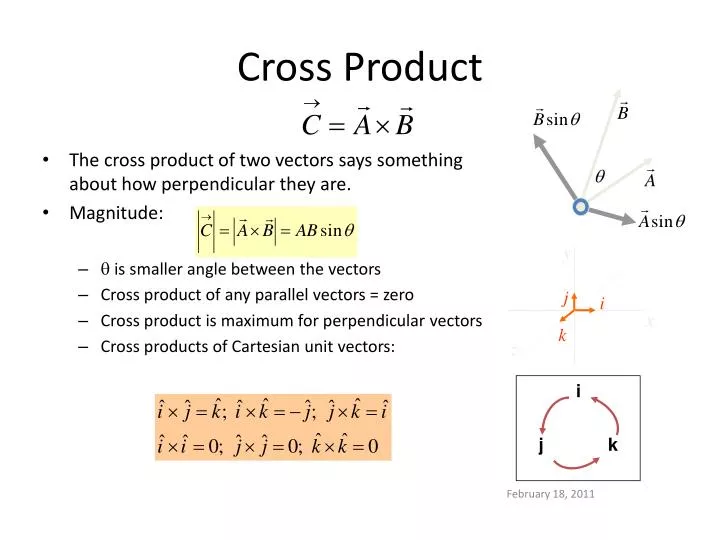
A b a a b b 0. A unit vector is often denoted by a lowercase letter with a circumflex or hat as in pronounced v hat. The term direction vector is used to describe a unit vector being used to represent spatial direction and such quantities are commonly denoted as d. As curl or rotation of two vectors give the direction of third vector.

I x j k. A vector is a mathematical construct that has magnitude and direction. Then i a sequence xn is c. This wave travels in the x direction with speed more specifically phase velocity.

2d spatial directions. Whenever x y xand λ k we have λx x. 3 if x is a k linear subspace of the k vector space v then x itself is a k vector space when equipped with the operations inherited from v. Therefore i x j 1 sin 90 k.

But j x i k because now the direction is reversed or due to vector identity a x b is not equal to. In this one dimensional example the direction of the wave vector is trivial. I j k. Prove than any linear subspace of v contains the zero vector 0 v 4 let v i i i be a family of k vector spaces indexed by a non empty set i.

I x j k j x k i k x i j j x i k k x j i i k j i x i 0 j x j 0 k x k 0. In mathematics a unit vector in a normed vector space is a vector often a spatial vector of length 1. The second row is the numerical coordinates of the first vector. Misc 5 find the value of x for which x 𝑖 𝑗 𝑘 is a unit vector let 𝑎 x 𝑖 𝑗 𝑘 so 𝑎 𝑥𝑖 𝑥𝑗 𝑥𝑘 given 𝑎 is a unit vector magnitude of 𝑎 is 1.

J k i k i j and so j i k etc 4. Then why i x j k this is because i along x axis and y along y axis thus angle between them will be 90 degree. The vector product is orthogonal to either factor. Let a a 1 i a 2 j a 3 k b b 1 i b 2 j b 3 k then a x b a 1 i a 2 j a 3 k x b 1 i b 2 j b 3 k the cross product of any two parallel vectors is the null vector since sin 0 0 and also i x j k j x k i k x i j and j x i k k x j.

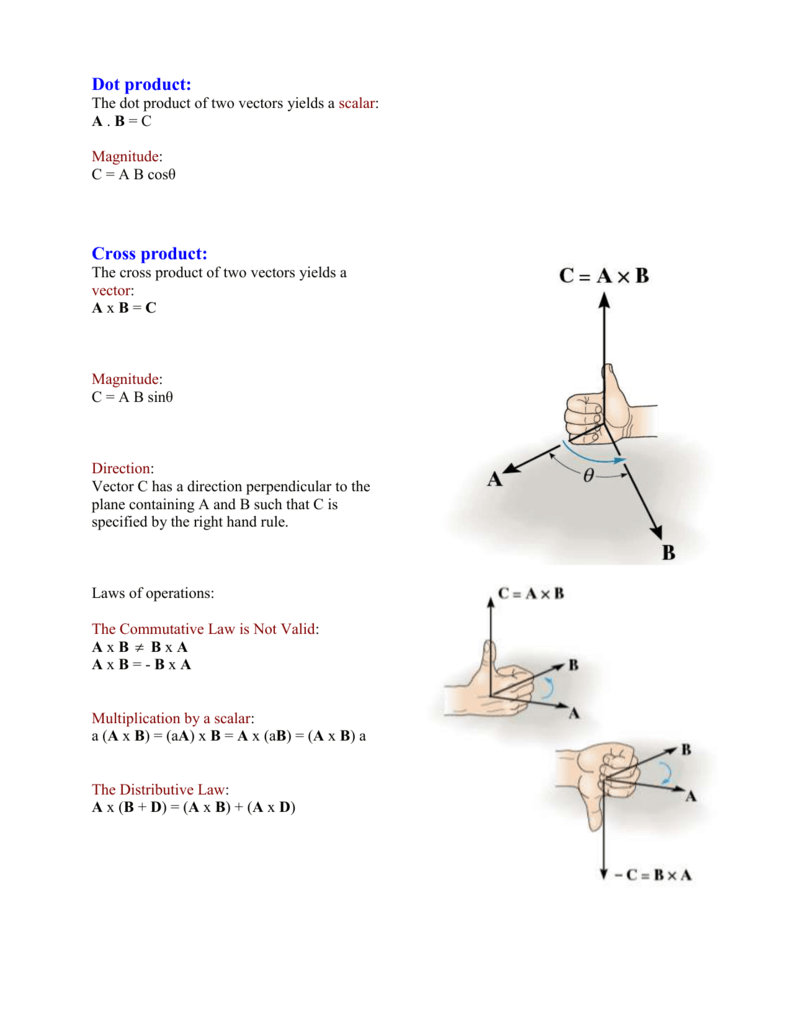
The cross product is done using a 3 x 3 determinant.